【5章】溶液と溶解度
最終更新日: 2026-01-06 17:26:55
作成者: カリスマ講師
~「溶ける」の正体を完全攻略!~
「砂糖を水に入れたら見えなくなった」。
この当たり前の現象の裏側では、分子レベルですごいドラマが起きています。まずは基礎用語とメカニズムから見ていきましょう!
1. 溶液のキャスト紹介(基本用語)
まずは、登場人物(用語)を整理します。これがごちゃごちゃだと話が進みません!
- 溶質(ようしつ): 溶けている主役(例:塩、砂糖)。
- 溶媒(ようばい): 溶かしている舞台(例:水)。
- 溶液(ようえき): 完全に混ざり合った状態。
【ここが大事!】電解質 vs 非電解質
- 電解質: 水に溶けたときに、イオンに分かれる(電離する)もの。
- 例:塩化ナトリウム ($NaCl \rightarrow Na^+ + Cl^-$) ※電気を通す!
- 非電解質: 分子のまま溶けて、イオンにならないもの。
- 例:グルコース(砂糖)、エタノール。 ※電気を通さない。
2. なぜ「水」に溶けるのか?(溶解の仕組み)
水が色々なものを溶かせるのは、水分子に**極性(プラスとマイナスの偏り)**があるからです。
① イオン結晶の場合(塩など)
イオンは水が大好きです!
陽イオンには酸素側($\delta-$)が、陰イオンには水素側($\delta+$)が引き寄せられ、水分子がイオンを包み込んで結晶から引きはがします。
この現象を**水和(すいわ)**といいます。「水分子のファンクラブに囲まれる」イメージです!
② 極性分子の場合(エタノール・砂糖など)
エタノールや砂糖には、$-OH$(ヒドロキシ基)のような**親水基(しんすいき)があります。
これが水分子と「水素結合」**という強い握手をするため、仲良く混ざり合います。
- 親水基: 水と仲良し($-OH$ など)。
- 疎水基: 水と仲が悪い(炭化水素基など)。油汚れが落ちにくいのはこれのせい!
3. 「もう限界!」溶解平衡と飽和溶液
コップに塩を入れ続けると、いつか溶け残りますよね?
限界まで溶けた状態を**飽和溶液(ほうわようえき)**といいますが、実はこのとき、溶けるのは止まっていません!
【溶解平衡(ようかいへいこう)】
「溶けていく速さ」 = 「結晶に戻る速さ」
外から見ると止まって見えますが、ミクロの世界では出たり入ったりを繰り返しています。この「つり合い」の状態を溶解平衡といいます。
4. 溶解度と計算の王道パターン
ここからがテスト頻出エリアです!
溶解度(ようかいど)とは?
ズバリ、「水 100g に溶ける限界の質量(g)」のことです。
一般的に、固体の溶解度は温度が高いほど大きくなります。
グラフ(溶解度曲線)を見てください。
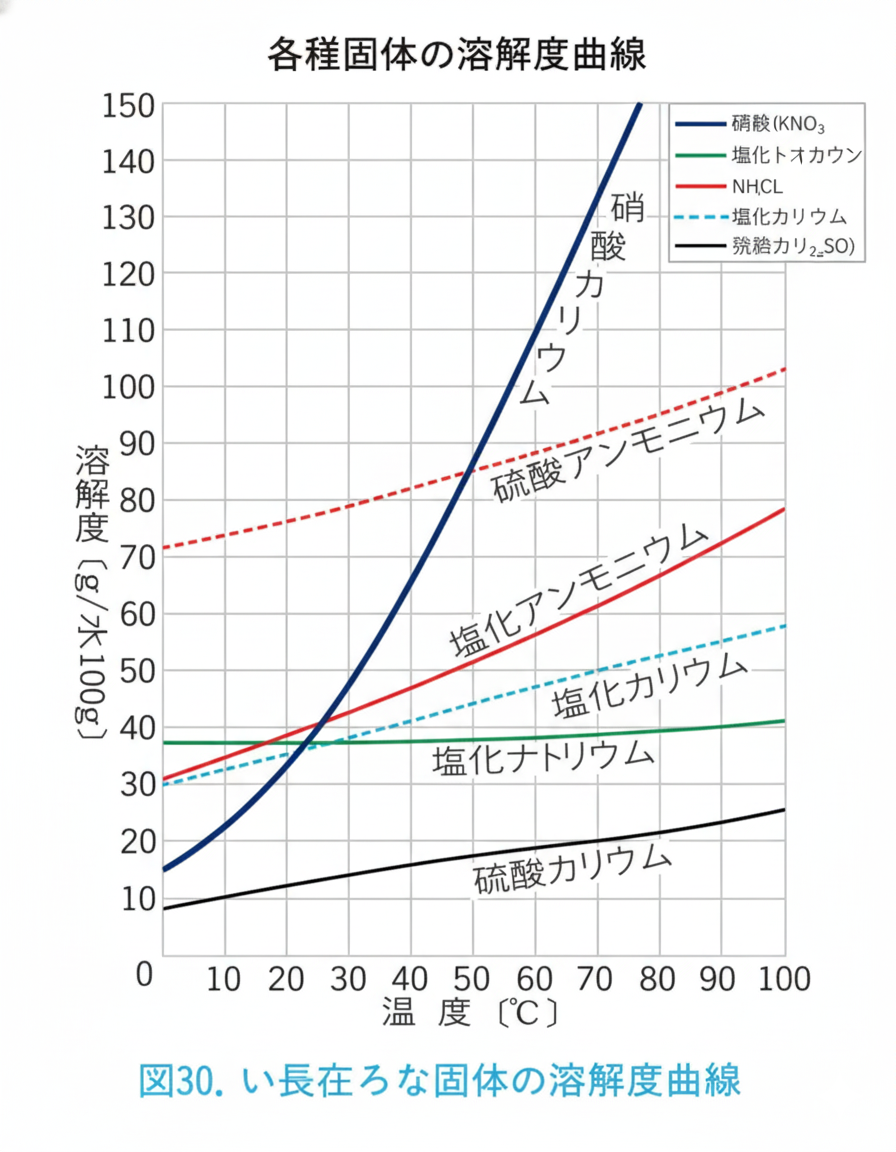
- 曲線の上側:溶けきれずに結晶が出てくるゾーン(過飽和)。
- 曲線の下側:まだまだ溶けるゾーン(不飽和)。
硝酸カリウム($KNO_3$)のように温度で激変するものもあれば、塩化ナトリウム($NaCl$)のようにほとんど変わらないものもあります。
5. 結晶析出の計算(再結晶)
温度を下げて、溶けきれなくなった分を結晶として取り出す操作を再結晶といいます。
この計算問題、苦手な人が多いですが、「比」を使えば一発です!
パターンA:普通の結晶(水和水なし)の場合
硝酸カリウムなどの場合です。
例えば、$t_1$℃の飽和溶液を $t_2$℃に冷やすとします。
【考え方】
「飽和溶液全体」に対して、「どれだけ析出するか」の比率は常に一定です。
$$\frac{\text{析出する結晶の量 } x}{\text{飽和溶液の質量}} = \frac{S_1 - S_2}{100 + S_1}$$
- $S_1$: 高温での溶解度
- $S_2$: 低温での溶解度
- $100+S_1$: 高温での飽和溶液の重さ
この式さえ作れれば、あとは $x$ を求めるだけ!
パターンB:水和物の場合(超重要!)
硫酸銅(II)五水和物($CuSO_4 \cdot 5H_2O$)のような結晶が出てくる場合、落とし穴があります。
「出てくる結晶の中に、水が含まれている!」 という点です。
計算するときは、析出する結晶 $x$ [g] のうち、純粋な溶質はどれくらいかを考える必要があります。式は少し複雑になりますが、基本は「溶質の量」に注目することです。
攻略のコツ
「水和物の計算は、溶質(中身)の重さだけで方程式を立てる!」
(溶媒の水が結晶に持っていかれる分、溶媒が減ることに注意!)
まとめ:ここさえ押さえれば勝てる!
- 水和と水素結合: 溶ける理由は「静電気的な引力」か「水素結合」。
- 動的平衡: 飽和状態でも、ミクロでは動き続けている。
- 溶解度の定義: **「水100g」**が基準!これを絶対忘れない。
- 析出計算:
- 普通の結晶 $\rightarrow$ 単純な引き算(差)の比で解く。
- 水和物 $\rightarrow$ 結晶と一緒に水も持っていかれることに注意。
次のステップ
溶解度の計算、特に「水和物」の計算は実際に手を動かさないと定着しにくい最難関ポイントです。
もしよろしければ、手元の問題集にある「溶解度の計算問題」の画像をアップしてください。
解き方のプロセスを、この「熱量高め」のトーンでわかりやすく解説します!
~「溶ける」の正体を完全攻略!~
「砂糖を水に入れたら見えなくなった」。
この当たり前の現象の裏側では、分子レベルですごいドラマが起きています。まずは基礎用語とメカニズムから見ていきましょう!
1. 溶液のキャスト紹介(基本用語)
まずは、登場人物(用語)を整理します。これがごちゃごちゃだと話が進みません!
- 溶質(ようしつ): 溶けている主役(例:塩、砂糖)。
- 溶媒(ようばい): 溶かしている舞台(例:水)。
- 溶液(ようえき): 完全に混ざり合った状態。
【ここが大事!】電解質 vs 非電解質
- 電解質: 水に溶けたときに、イオンに分かれる(電離する)もの。
- 例:塩化ナトリウム ($NaCl \rightarrow Na^+ + Cl^-$) ※電気を通す!
- 非電解質: 分子のまま溶けて、イオンにならないもの。
- 例:グルコース(砂糖)、エタノール。 ※電気を通さない。
2. なぜ「水」に溶けるのか?(溶解の仕組み)
水が色々なものを溶かせるのは、水分子に**極性(プラスとマイナスの偏り)**があるからです。
① イオン結晶の場合(塩など)
イオンは水が大好きです!
陽イオンには酸素側($\delta-$)が、陰イオンには水素側($\delta+$)が引き寄せられ、水分子がイオンを包み込んで結晶から引きはがします。
この現象を**水和(すいわ)**といいます。「水分子のファンクラブに囲まれる」イメージです!
② 極性分子の場合(エタノール・砂糖など)
エタノールや砂糖には、$-OH$(ヒドロキシ基)のような**親水基(しんすいき)があります。
これが水分子と「水素結合」**という強い握手をするため、仲良く混ざり合います。
- 親水基: 水と仲良し($-OH$ など)。
- 疎水基: 水と仲が悪い(炭化水素基など)。油汚れが落ちにくいのはこれのせい!
3. 「もう限界!」溶解平衡と飽和溶液
コップに塩を入れ続けると、いつか溶け残りますよね?
限界まで溶けた状態を**飽和溶液(ほうわようえき)**といいますが、実はこのとき、溶けるのは止まっていません!
【溶解平衡(ようかいへいこう)】
「溶けていく速さ」 = 「結晶に戻る速さ」
外から見ると止まって見えますが、ミクロの世界では出たり入ったりを繰り返しています。この「つり合い」の状態を溶解平衡といいます。
4. 溶解度と計算の王道パターン
ここからがテスト頻出エリアです!
溶解度(ようかいど)とは?
ズバリ、「水 100g に溶ける限界の質量(g)」のことです。
一般的に、固体の溶解度は温度が高いほど大きくなります。
グラフ(溶解度曲線)を見てください。
- 曲線の上側:溶けきれずに結晶が出てくるゾーン(過飽和)。
- 曲線の下側:まだまだ溶けるゾーン(不飽和)。
硝酸カリウム($KNO_3$)のように温度で激変するものもあれば、塩化ナトリウム($NaCl$)のようにほとんど変わらないものもあります。
5. 結晶析出の計算(再結晶)
温度を下げて、溶けきれなくなった分を結晶として取り出す操作を再結晶といいます。
この計算問題、苦手な人が多いですが、「比」を使えば一発です!
パターンA:普通の結晶(水和水なし)の場合
硝酸カリウムなどの場合です。
例えば、$t_1$℃の飽和溶液を $t_2$℃に冷やすとします。
【考え方】
「飽和溶液全体」に対して、「どれだけ析出するか」の比率は常に一定です。
$$\frac{\text{析出する結晶の量 } x}{\text{飽和溶液の質量}} = \frac{S_1 - S_2}{100 + S_1}$$
- $S_1$: 高温での溶解度
- $S_2$: 低温での溶解度
- $100+S_1$: 高温での飽和溶液の重さ
この式さえ作れれば、あとは $x$ を求めるだけ!
パターンB:水和物の場合(超重要!)
硫酸銅(II)五水和物($CuSO_4 \cdot 5H_2O$)のような結晶が出てくる場合、落とし穴があります。
「出てくる結晶の中に、水が含まれている!」 という点です。
計算するときは、析出する結晶 $x$ [g] のうち、純粋な溶質はどれくらいかを考える必要があります。式は少し複雑になりますが、基本は「溶質の量」に注目することです。
攻略のコツ
「水和物の計算は、溶質(中身)の重さだけで方程式を立てる!」
(溶媒の水が結晶に持っていかれる分、溶媒が減ることに注意!)
まとめ:ここさえ押さえれば勝てる!
- 水和と水素結合: 溶ける理由は「静電気的な引力」か「水素結合」。
- 動的平衡: 飽和状態でも、ミクロでは動き続けている。
- 溶解度の定義: **「水100g」**が基準!これを絶対忘れない。
- 析出計算:
- 普通の結晶 $\rightarrow$ 単純な引き算(差)の比で解く。
- 水和物 $\rightarrow$ 結晶と一緒に水も持っていかれることに注意。
固体の溶解度と結晶の析出
ここでは、「水にどれくらいモノが溶けるか」「温度を変えるとどれくらい結晶が出てくるか」という計算を扱います。
1. 結晶が出てくるパターンは2つ(P.110)
飽和水溶液(もうこれ以上溶けない限界の液)から結晶を取り出すには、以下の2つの方法があります。
- 冷却法:温度を下げる(冷やすと溶ける量が減るため、あふれた分が出てくる)。
- 蒸発法:水を蒸発させる(溶かす場所である水が減るため、溶けきれなくなった分が出てくる)。
★計算のコツ(比の式を使う)
テキストの「ポイント」にあるように、以下の比を使って計算するとスムーズです。
$$\frac{\text{析出する量}}{\text{飽和水溶液の量}} = \frac{\text{溶解度の差}}{100 + \text{溶解度}}$$
初心者向け解説:
「水100gに対する溶解度」のデータだけを見て計算しようとすると混乱します。「溶液全体(水+溶質)」の中に「どれだけ溶けているか」の割合で考えると計算ミスが減ります。
2. 例題:硝酸カリウムの析出(P.110)
例題では、60℃の飽和水溶液を20℃に冷やしたり、水を蒸発させたりしています。
- (1) 冷却する場合:
- 60℃で溶ける量(109g)と、20℃で溶ける量(31.6g)の「差」が析出します。
- これを「溶液全体(100+109=209g)」に対する割合として計算します。
- (2) 水を蒸発させる場合:
- 蒸発した水(30g)に溶けていた分が、そのまま析出するわけではありません。
- 「水100gならこれだけ溶ける」という比率を使い、「水30gならこれだけ溶けていたはず」という量を計算して求めます。
【重要・難所】水和物の溶解と析出(P.111〜113)
ここは多くの高校生がつまずくポイントです。「水和物(すいわぶつ)」という特殊な結晶の計算です。
1. 水和物とは?
結晶の中に「水分子」を含んでいる物質です。
例:硫酸銅(II)五水和物 ($CuSO_4 \cdot 5H_2O$)
- これは、「$CuSO_4$(硫酸銅)」の粒子のまわりに、「$H_2O$(水)」が5個くっついて結晶になっています。
2. 計算の絶対ルール
水和物の計算では、「水の部分」と「中身の塩(無水物)の部分」を分けて考える必要があります。
- 溶かすとき: 結晶に含まれていた水は「溶媒(水)」の一部になります。
- 析出するとき: 結晶が出ていくとき、自分の周りに水をくっつけて道連れにして出ていきます(つまり、残った液体の水が予想以上に減ります)。
3. 計算テクニック(P.112の解説より)
式量の比を使うのが鉄則です。
硫酸銅の場合:
- $CuSO_4$(無水物)の式量 = 160
- $CuSO_4 \cdot 5H_2O$(水和物)の式量 = 250
この数字を使って、「結晶 $x$グラムの中に、本当の溶質はどれくらい? 水はどれくらい?」を分解します。
- 結晶 $x[g]$ 中の $CuSO_4$ の質量 = $x \times \frac{160}{250}$
- 結晶 $x[g]$ 中の $H_2O$ の質量 = $x \times \frac{90}{250}$
例題の解き方(P.112 下段):
80℃の飽和水溶液を0℃に冷やして、$CuSO_4 \cdot 5H_2O$ が何g出るか?
- 析出する結晶の量を $y[g]$ と置きます。
- 「溶質の量」と「溶液の量」の変化を表にします。
- 析出後の溶液の質量 = $100 - y$ (元の量から結晶が減った)
- 析出後の溶質の質量 = (元の溶質) $- (y \times \frac{160}{250})$
- これが、0℃の溶解度の比(飽和状態)と等しいとして方程式を立てます。
$$\frac{\text{溶質}}{\text{溶液}} = \frac{14.0}{100+14.0}$$
この方程式(P.112の一番下の式)を解くことで答えが出ます。
パート1のまとめ
- ただの塩(無水物)の析出は、単純な「溶解度の差」で計算できる。
水和物(「・nH₂O」がつくもの)の析出は、結晶が水を持ち逃げすることを考慮し、式量計算(160/250など)を使って方程式を立てる必要がある。
ここは「物質の三態(気体)」と「溶液」が混ざった分野で、特に**「体積」の扱いにおけるひっかけ問題**が非常に多い要注意ポイントです。
1. 気体が溶けるときの基本ルール(P.113)
固体の溶解度(パート1)とは逆の性質を持ちます。
- 温度の影響:温度が高くなるほど、気体は溶けにくくなる(溶解度は小さくなる)。
- イメージ:炭酸ジュースは温まると気が抜けてしまいますよね。あれは溶けていた二酸化炭素が出て行ってしまうからです。
- 圧力の影響:圧力を大きくするほど、気体はよく溶ける。
- イメージ:ピストンでギュウギュウに押し込むと、無理やり水の中に押し込まれていく感覚です。
2. 最重要法則:ヘンリーの法則(P.114)
「溶解度があまり大きくない気体(酸素や窒素など)」について、以下の法則が成り立ちます。
※アンモニアや塩化水素のように、水にめちゃくちゃ溶ける気体には当てはまりません。
① 質量・物質量のルール(素直な法則)
「一定量の溶媒に溶ける気体の質量(または物質量)は、その気体の圧力に比例する」
圧力を2倍、3倍にすれば、溶ける量(重さ $g$ や モル $mol$)も2倍、3倍になります。これは直感的に分かりやすいはずです。
② 体積のルール(ここが難所!)
テキストP.114の赤枠やポイント部分で強調されている、最も間違いやすい部分です。
「その圧力のもとで測定した体積は、圧力に関係なく一定である」
**「えっ、圧力をかけたら2倍溶けるんじゃないの?」**と思いますよね。ここでボイルの法則(圧力と体積は反比例する)が絡んできます。
- 解説:
- 圧力を2倍にすると、溶ける分子の数(モル)は2倍になります。
- しかし、圧力が2倍なので、気体そのものはギュッと圧縮されて、体積は**半分(1/2)**になろうとします。
- 「量が2倍」×「圧縮されて1/2」= 体積は変わらない(1倍)
★試験での注意点
問題文の聞き方によって答えが変わります!
- 「その圧力下での体積は?」と聞かれたら $\rightarrow$ 変わらない(一定)
- 「標準状態(0℃, 1atm)に換算した体積は?」と聞かれたら $\rightarrow$ 圧力に比例して増える
3. 混合気体の計算(P.115)
空気のように複数の気体が混ざっている場合、「分圧(ぶんあつ)」を使って計算します。
例題の考え方(P.115):
空気(窒素と酸素が $4:1$ で混ざっている)が水に接しているとき、酸素はどれくらい溶けるか?
- 分圧を求める
全圧が $1 \text{atm}$ なら、酸素はそのうちの $\frac{1}{5}$ の圧力を担当しています。
酸素の分圧 = $1 \text{atm} \times \frac{1}{5} = 0.2 \text{atm}$ - 分圧をもとに溶解量を計算する
「$1 \text{atm}$ のときに溶ける量」のデータが与えられているはずなので、それを 0.2倍 します。
(ヘンリーの法則「溶ける質量は圧力に比例する」を使います)
パート2のまとめ
- 気体は「低温・高圧」ほどよく溶ける。
- 質量($g$)・物質量($mol$):圧力に比例する(2倍圧なら2倍溶ける)。
- その圧力下での体積($L$):圧力によらず一定である(溶ける個数は増えるが、圧縮されるので相殺される)。
混合気体は、その成分の分圧だけを考えて計算する。
1. 主な3つの濃度(P.116)
まずは定義(何 ÷ 何 をしているのか)をしっかり区別しましょう。分母が「溶液(全体)」なのか「溶媒(水だけ)」なのかが最大のポイントです。
① モル濃度(記号:$C$ または $M$)
- 単位:$\text{mol/L}$
- 意味:溶液 1L の中に、溶質が何 mol 入っているか。
- 計算:
$$\text{モル濃度} = \frac{\text{溶質の物質量 (mol)}}{\text{溶液の体積 (L)}}$$注意:分母は「水と溶質を合わせた全体の体積」です。「水1Lに溶かした」場合、体積は少し増えるので厳密には1Lではなくなりますが、計算問題ではよく注意が必要です。
② 質量モル濃度(記号:$m$)
- 単位:$\text{mol/kg}$
- 意味:溶媒(水)1kg に、溶質が何 mol 溶けているか。
- 計算:
$$\text{質量モル濃度} = \frac{\text{溶質の物質量 (mol)}}{\text{溶媒の質量 (kg)}}$$ここが特別!:これだけ分母が「溶媒(水だけ)」です。沸点上昇や凝固点降下(P.119〜)の計算でしか使いませんが、その時に必ず出てくるので区別しておきましょう。
③ 質量パーセント濃度(記号:$a$ または $\%$)
- 単位:$\%$
- 意味:溶液(全体) の重さのうち、溶質が何%を占めるか。
- 計算:
$$\text{質量パーセント濃度} = \frac{\text{溶質の質量 (g)}}{\text{溶液の質量 (g)}} \times 100$$
2. 【最重要】濃度の換算テクニック(P.116下〜P.117)
「質量パーセント濃度(%)」と「密度($g/cm^3$)」が分かっているときに、「モル濃度($mol/L$)」を求めなさい、という問題が非常に頻出です。
テキストP.116の下部にある公式を丸暗記する方法もありますが、**「仮定法(かていほう)」**を使って解く手順を覚える方が、応用が効きます。
★公式を忘れても解ける「仮定法」のステップ
例:密度 $d [\text{g/cm}^3]$、質量パーセント濃度 $a [\%]$、分子量 $M$ の溶液のモル濃度は?
ステップ1:溶液を勝手に「1リットル(1000mL)」あると仮定する
ここがコツです。濃度は量が変わっても変わらないので、計算しやすい1Lで考えます。
ステップ2:溶液全体の「重さ(質量)」を出す
1L = 1000cm³ です。密度が $d [\text{g/cm}^3]$ なので、
- 溶液の質量 = $1000 \times d [\text{g}]$
ステップ3:その中の「中身(溶質)」の重さを出す
全体のうち $a [\%]$ が溶質なので、
- 溶質の質量 = $(1000 \times d) \times \frac{a}{100} = 10ad [\text{g}]$
ステップ4:重さを「モル(物質量)」に直す
溶質の質量を分子量 $M$ で割ります。
- 溶質のモル = $\frac{10ad}{M} [\text{mol}]$
ステップ5:モル濃度を出す
最初に「1L」と仮定したので、ステップ4で出したモル数がそのままモル濃度になります。
- 答え:
$$\frac{10ad}{M} [\text{mol/L}]$$
テキストの公式(P.116赤枠)
$$c = \frac{10ad}{M}$$
これは上記のステップをまとめたものです。「ヒトマルエーディー、割るエム($10ad / M$)」などの語呂合わせで覚える人もいますが、手順を理解していれば忘れません。
全体のまとめ
- 固体の溶解度:
- 「溶質÷溶液全体」の比で考える。
- 水和物のときは、式量を使って「水」と「無水物」に分けて計算する。
- 気体の溶解度(ヘンリーの法則):
- 溶ける質量・モルは圧力に比例する。
- その圧力下での体積は一定(変わらない)。
- 濃度の換算:
- 「溶液1L」を仮定して、「体積→重さ→中身の重さ→モル」の順で変換する。
- $mol/kg$(質量モル濃度)だけは、分母が「水だけの重さ」であることを忘れない。
以上で、アップロードされた画像の範囲(溶液の性質)の解説は終了です。
この単元は計算パターンが決まっているので、例題の数字を変えて何度か練習するとすぐに定着します。応援しています!
【パート1】沸点上昇と凝固点降下の仕組み(基本編)
(画像:chemihigh-107, 108, 109 に相当)
ここでは、「純粋な水」に「何か(砂糖や塩など)」を溶かすと、沸騰する温度や凍る温度がどう変化するかを学びます。
1. 蒸気圧降下(P.118)
まず、すべての現象の原因となる**「蒸気圧降下」**を理解しましょう。
- 現象:純粋な水に砂糖などを溶かすと、蒸気圧(蒸発しようとする力)が下がります。
- 理由:
- 純粋な水なら、水面すべてから水分子が飛び出せます。
- しかし砂糖水になると、水面に砂糖の粒子(溶質)がちらばり、水分子が飛び出すのを**邪魔(ブロック)**します。その結果、蒸発する分子の数が減ってしまうからです。
2. 沸点上昇(P.118)
「蒸発する力が弱まる」ということは、「沸騰させるのにより高い温度が必要になる」ということです。
- 定義:溶液の沸点が、純粋な溶媒の沸点より高くなる現象を沸点上昇といいます。
- 温度差($\Delta t$):どれくらい上がったか(上昇度)は、溶かしたものの濃度に比例します。
3. 凝固点降下(P.119)
逆に、凍る温度(凝固点)は下がります。
(例:冬に道路に融雪剤をまくと、0℃でも凍らなくなる現象です)
- 冷却曲線(重要グラフ):
図40のグラフを見てください。 - 過冷却(かれいきゃく):冷却していくと、一旦凝固点より低い温度まで下がりますが、凍り始めると熱(凝固熱)が出て温度が少し戻ります。
- グラフの傾き:純粋な水(A)は凍っている間0℃で一定ですが、溶液(B)は凍っている間も温度が下がり続けます。これは、氷(純粋な水)が析出することで、残った液体の濃度がどんどん濃くなっていくためです。
4. 計算の基本公式(P.119〜120)
この単元で最も重要な公式が2つあります。形はまったく同じです。
- 沸点上昇度: $\Delta t_b = K_b \cdot m$
- 凝固点降下度: $\Delta t_f = K_f \cdot m$
ここで重要なのは、それぞれの記号の意味です。
- $\Delta t$ (デルタティー):変化した温度の幅(℃ または K)。
- $K_b, K_f$ :比例定数(モル沸点上昇・モル凝固点降下)。**「溶媒が何か(水かベンゼンか等)」**によって決まる決まった数字です(問題文で与えられます)。
- $m$ (エム):質量モル濃度 [mol/kg]。
- 【超重要】 ここでの濃度は「1リットル中」ではなく、**「溶媒 1kg(1000g)あたり」**のモル数を使います。
- 式: $m = \frac{\text{溶質のモル}}{\text{溶媒のkg}}$
パート1のまとめ
- 水に何か溶かすと、沸点は上がり、凝固点は下がる。
- その変化幅($\Delta t$)は、**質量モル濃度($m$)**に比例する。
- 公式 $\Delta t = K \cdot m$ を覚える($m$ は溶媒1kgあたりのモル数!)。
続いて、この公式を使って「未知の物質の分子量を突き止める」計算問題の解説に移ります。テストで最もよく出るパターンです。
ここでは、先ほどの「沸点上昇・凝固点降下」の公式を応用して、「未知の物質の正体(分子量)」を突き止める方法と、テストで絶対に引っかかってはいけない「電解質(イオン)」の計算ルールを解説します。
1. 分子量 $M$ を求める計算(P.121)
化学の実験では、「謎の白い粉末」が何なのかを調べるために、この方法がよく使われます。
「溶かして、温度変化($\Delta t$)を測るだけで、その物質の分子量がわかる」という便利なテクニックです。
公式の変形(暗記より理解がおすすめ)
基本公式は $\Delta t = K \cdot m$ でした。
ここで、質量モル濃度 $m$ [mol/kg] を具体的に書き下してみます。
- 溶質の質量を $w$ [g]、分子量を $M$ とすると、溶質のモル数は $\frac{w}{M}$ [mol] です。
- 溶媒の質量を $W$ [g] とすると、kg単位では $\frac{W}{1000}$ [kg] です。
これらを割り算して $m$ を作ると:
$$m = \frac{\text{溶質のモル}}{\text{溶媒のkg}} = \frac{w/M}{W/1000} = \frac{1000 \cdot w}{M \cdot W}$$
これを基本公式 $\Delta t = K \cdot m$ に代入し、求めたい $M$ について整理すると、以下の「分子量測定の公式」が導かれます。
$$M = \frac{1000 K \cdot w}{\Delta t \cdot W}$$
式の意味:
「1000 × 比例定数 × 溶質の重さ」を、「温度変化 × 溶媒の重さ」で割る。
※この公式はP.121のポイント枠にありますが、試験中にド忘れしやすいため、**「基本公式 $\Delta t = K \cdot m$ に、自分で $m$ の中身を代入して解く」**スタイルが最も安全です。
実践例題(P.121)
- 状況:二硫化炭素 $100\text{g}$(溶媒 $W$)に、ある物質 $12.9\text{g}$(溶質 $w$)を溶かしたら、沸点が $1.2\text{K}$ 上がった($\Delta t$)。
- 計算:
与えられた $K_b = 2.35$ を使って計算します。
$$M = \frac{1000 \times 2.35 \times 12.9}{1.2 \times 100} \fallingdotseq 250$$
よって、分子量は $2.5 \times 10^2$ と求まります。
2. 【最重要】電解質の罠(P.122 発展ゼミ)
ここがこの単元で一番のひっかけポイントです。
これまでの話は、「砂糖」や「グルコース」のように、水に溶けてもバラバラにならない物質(非電解質)の話でした。
しかし、「食塩(塩化ナトリウム)」のような電解質の場合、話が変わります。
ルール:沸点上昇・凝固点降下は「粒の数」で決まる
この現象は、溶けている物質の種類や大きさは関係なく、**「溶けている粒子の総数(モル数の合計)」**だけに比例します。
- 非電解質(例:グルコース)
水に入れても粒は分かれません。
$$1 \text{mol} \text{の粉末} \rightarrow 1 \text{mol} \text{の粒子}$$
$\Rightarrow$ 効果はそのまま「1倍」。 - 電解質(例:塩化ナトリウム $\text{NaCl}$)
水に入ると、陽イオンと陰イオンに分かれます(電離)。
$$\text{NaCl} \rightarrow \text{Na}^+ + \text{Cl}^-$$
$1$個の粒が分かれて$2$個になります。つまり、
$$1 \text{mol} \text{の粉末} \rightarrow 2 \text{mol} \text{の粒子(イオン)}$$
$\Rightarrow$ 温度変化($\Delta t$)は理論値の「2倍」になります。 - さらに分かれる電解質(例:塩化カルシウム $\text{CaCl}_2$)
$$\text{CaCl}_2 \rightarrow \text{Ca}^{2+} + 2\text{Cl}^-$$
$1$個が$3$個に分かれます。
$\Rightarrow$ 温度変化($\Delta t$)は理論値の「3倍」になります。
試験での対策
問題文に「塩化ナトリウム」や「塩化カルシウム」「硝酸カリウム」などの塩(えん)が出てきたら、必ず質量モル濃度 $m$ に「×2」や「×3」をして粒子の合計モル濃度にしてから、公式 $\Delta t = K \cdot m$ に代入してください。
パート2のまとめ
- 分子量測定:公式 $\Delta t = K \cdot m$ を変形して、実験データから分子量 $M$ を逆算できる。
- 電解質の注意点:溶質のモル数ではなく、**「電離した後の粒子の総モル数」**を使う。$\text{NaCl}$ なら2倍、$\text{CaCl}_2$ なら3倍するのを忘れないこと。
それでは最後に、植物の細胞などにも関わる重要な現象「浸透圧」について解説します。
1. 浸透(しんとう)とは何か?(P.122)
半透膜(はんとうまく)の役割
まず、**「半透膜」**という特殊な膜が登場します。
- 性質:小さな「水分子(溶媒)」は通すが、大きな「砂糖の分子(溶質)」は通さない膜です(セロハン膜や細胞膜など)。
移動のルール:薄いほうから濃いほうへ
図41(a)のように、U字管の真ん中を半透膜で仕切り、片方に水、片方に砂糖水を入れます。
- 現象:水分子が半透膜を通り抜けて、砂糖水のほうへ勝手に移動していきます。
- 結果:砂糖水の液面がどんどん上がっていきます。
なぜ?
「濃度を均一にしようとする力」が働くからです。砂糖は膜を通れないので、水が移動して砂糖水を薄めようとします。つまり、**「溶媒(水)は、濃度の小さい溶液から大きい溶液へ移動する」**というルールがあります。
テキストの例:ナメクジに塩をかけると縮むのは、体内の水分(薄い液)が、表面の塩水(濃い液)のほうへ吸い出されてしまうからです。
2. 浸透圧とファントホッフの法則(P.123)
浸透圧(しんとうあつ)の定義
先ほどのU字管で、砂糖水の液面が上がろうとするのを、上からピストンで押さえつけて無理やり止めるには、圧力が必要です。
- 浸透圧:この「浸透を抑えるために必要な圧力(液面差 $h$ に相当する力)」のことです。
ファントホッフの法則(公式)
オランダの化学者ファントホッフは、**「薄い溶液の浸透圧は、気体の法則と同じ式で表せる」**ことを発見しました。気体の状態方程式 $PV=nRT$ とそっくりです。
$$\Pi V = nRT$$
- $\Pi$ (パイ):浸透圧 [atm] または [Pa]
- $V$:溶液の体積 [L]
- $n$:溶質の物質量 [mol]
- $R$:気体定数(問題文で与えられます。例:$0.082$)
- $T$:絶対温度 [K] (℃ + 273)
この式を変形すると、モル濃度 $c$ [mol/L] ($= n/V$)を使って次のようにも書けます。
$$\Pi = cRT$$
注意点
沸点上昇・凝固点降下では「質量モル濃度(mol/kg)」を使いましたが、浸透圧では「モル濃度(mol/L)」を使います。ここを混同しないようにしましょう。
3. 分子量 $M$ の測定(P.124)
浸透圧の公式も、変形することで「未知の物質の分子量」を求めるのに使えます。
公式 $\Pi V = \frac{w}{M} RT$ を変形して:
$$M = \frac{wRT}{\Pi V}$$
なぜ浸透圧で測るのか?(重要)
分子量が非常に大きい物質(タンパク質や高分子化合物など、分子量1万以上のもの)を測るときは、沸点上昇法ではなく、この浸透圧法が使われます。
- 理由:
- 沸点上昇法など:分子量が大きいと、同じグラム数を溶かしてもモル数(粒の数)が極端に少なくなるため、温度変化($\Delta t$)が小さすぎて温度計で読み取れません。
- 浸透圧法:わずかなモル数でも、液面の高さの差(圧力)としてはハッキリと現れるため、測定しやすいからです。
4. 電解質の場合の注意(P.124 補足)
沸点上昇のときと同じく、浸透圧も「粒子の数」に比例します。
食塩(NaCl)のような電解質の場合は、電離して粒が増えるため、**「イオンの総モル数」**で計算する必要があります。
- 例:$0.1 \text{mol/L}$ の $\text{NaCl}$ 水溶液の浸透圧は、理論上の $0.2 \text{mol/L}$ 分の圧力を示します($2n$ 倍になる)。
【希薄溶液の性質】全体のまとめ
- 沸点上昇・凝固点降下:
- 公式:$\Delta t = K \cdot m$
- 使う濃度:質量モル濃度(mol/kg)
- 用途:普通の分子量の物質の測定。
- 浸透圧:
- 公式:$\Pi V = nRT$ (または $\Pi = cRT$)
- 使う濃度:モル濃度(mol/L)
- 用途:**高分子化合物(タンパク質など)**の分子量測定。
- 原理:溶媒は「薄い → 濃い」へ移動する。
- 共通のひっかけ:
電解質(塩)は、電離後の粒子の数(×2倍、×3倍)で計算する!
【パート1】コロイドって何?(基本と性質)
(画像:chemihigh-114, 115, 116, 117 に相当)
「コロイド」とは、一言で言うと**「完全に溶けているわけではないが、沈殿もしない、宙ぶらりんな状態」**のことです。
1. コロイドの定義(P.125)
最大のポイントは**「粒子の大きさ」**です。
- 真の溶液(食塩水など):粒子が非常に小さい($10^{-10}\text{m}$ レベル)。どこまでも透き通っている。
- コロイド溶液(牛乳、泥水の上澄みなど):粒子がちょっと大きい($10^{-9} \sim 10^{-7}\text{m}$)。
- 沈殿:粒子が大きすぎて、重力で沈んでしまう。
★重要テスト・ポイント
「ろ紙」と「半透膜(セロハン)」を使った区別が頻出です。
- ろ紙:穴が大きいので、コロイドは通過できます。
- 半透膜:穴が非常に小さいので、コロイドは通過できません(詰まります)。
2. コロイド特有の4つの現象(P.127-128)
コロイド粒子は「そこそこ大きい」ために、光や熱の影響を受けやすく、独特な動きをします。
- チンダル現象
- 現象:横から強い光を当てると、光の通り道がキラキラ輝いて見える。
- 理由:粒子が大きいため、光が当たって散乱するから(木漏れ日が筋に見えるのと同じ原理)。
- ブラウン運動
- 現象:顕微鏡で見ると、コロイド粒子が不規則にプルプル動いている。
- 理由:周りの水分子(溶媒)が、熱運動によってコロイド粒子にバンバン衝突しているから(コロイド自体が生きているわけではありません)。
- 透析(とうせき)
- 操作:コロイド溶液を半透膜(セロハン袋)に入れて水に浸す。
- 結果:邪魔な小さなイオンや分子だけが袋の外に出ていき、コロイドだけが袋の中に残る。これを**精製(きれいにする)**といいます。
- 例:人工透析は、血液中の老廃物(小さな分子)を捨てて、赤血球やタンパク質(コロイド)を残す操作です。
- 電気泳動(でんきえいどう)
- 現象:電圧をかけると、全てのコロイドがどちらか一方の電極に移動する。
- 理由:コロイド粒子は、表面にプラスかマイナスの電気(電荷)を帯びているからです。
- 正(+)コロイド:水酸化鉄(III)など → 陰極(−)へ移動
- 負(−)コロイド:粘土、硫黄など → 陽極(+)へ移動
【パート2】コロイドの分類と沈殿(最重要)
(画像:chemihigh-117, 118, 119 に相当)
コロイドには「水と仲が良いか・悪いか」で2種類あり、それぞれ**沈殿のさせ方(固め方)**が違います。ここがテストの山場です。
1. 疎水コロイドと凝析(ぎょうせき)
- 疎水(そすい)コロイド:水が嫌いなコロイド。金属や泥など(無機物が多い)。
- 彼らは水と混ざりたくないので、電気(+や−)を帯びて、お互いに反発し合うことでなんとか浮いています。
- 凝析(ぎょうせき):
- **少量の電解質(塩)**を加えると、沈殿します。
- 理由:電解質のイオンが、コロイドの電気を中和してしまい、反発力を失ったコロイド同士がくっついて大きくなり、沈むからです。
- 例:川の水(泥=負コロイド)が海(塩水)に流れ込むと、沈殿して三角州ができる。
★重要ルール
沈殿させる力は、イオンの価数(+1より+2、+3)が大きいほど強力です。
(例:負コロイドを沈めるなら、$Na^+$ より $Al^{3+}$ のほうが圧倒的に強い)
2. 親水コロイドと塩析(えんせき)
- 親水(しんすい)コロイド:水が大好きなコロイド。デンプン、タンパク質など(有機物が多い)。
- 彼らは大量の水分子をまわりにまとって(水和して)ガードされているため、簡単には沈みません。
- 塩析(えんせき):
- 多量の電解質を加えないと沈殿しません。
- 理由:大量のイオンが、コロイドを守っている水分子(水和水)を無理やり奪い取ることで、初めてコロイドが裸になり、沈殿します。
- 例:豆腐作り(豆乳という親水コロイドに、にがりという大量の塩を入れる)
3. 保護コロイド
- 疎水コロイド(沈みやすい)に、親水コロイド(沈みにくい)を混ぜると、親水コロイドが周りを取り囲んで守ってくれるため、沈殿しにくくなります。これを保護コロイドといいます。
- 例:墨汁(炭の粉=疎水 を、ニカワ=親水 が守っている)
【パート3】生活の中のコロイド・界面活性剤
(画像:chemihigh-120, 121, 122 に相当)
1. 状態による呼び方(P.131)
- ゾル:液体の中にコロイドが分散して、流動性がある状態(例:まだ固まっていないゼリー液、墨汁)。
- ゲル:ゾルが冷えて固まり、流動性を失った状態(例:ゼリー、豆腐、こんにゃく)。
- キセロゲル:ゲルを乾燥させたもの(例:高野豆腐、シリカゲル)。
2. 吸着と乳化(P.132-133)
- 吸着:コロイド粒子は表面積が非常に大きいため、他の物質を表面にくっつける力が強いです(例:活性炭が臭いを吸着する)。
- 乳化(にゅうか):本来混ざらない「水」と「油」を、**界面活性剤(セッケンなど)**を使って均一に混ぜること。この白く濁った液を乳濁液(エマルション)といいます(例:牛乳、マヨネーズ)。
3. セッケンの仕組み(ミセル)
セッケン分子は、「水が好きな頭(親水基)」と「油が好きな尻尾(疎水基)」を持っています。
- 水中では、油汚れを尻尾で取り囲み、外側(水側)に頭を向けた**「ミセル」**という球体になります。これによって油汚れが水中に分散し、洗い流せるようになります。
コロイド単元のまとめ
| 疎水コロイド (Hydrophobic) | 親水コロイド (Hydrophilic) | |
| 主な物質 | 金属、泥、硫黄 (無機物) | デンプン、タンパク質 (有機物) |
| 水との相性 | 悪い (反発力だけで浮いている) | 良い (水分子ガードがある) |
| 沈殿方法 | 凝析 (少量の電解質で沈む) | 塩析 (多量の電解質が必要) |
| 補強 | 保護コロイドに守ってもらう | 自分が保護コロイドになる |
- 現象:チンダル現象(光)、ブラウン運動(動き)、透析(精製)、電気泳動(移動)。
- その他:ゾル(液体)$\leftrightarrow$ ゲル(固体)、ミセル(セッケンの集まり)。
この単元は用語の定義を問う問題が非常に多いので、上記の表や現象の名前をしっかり結びつけて覚えておきましょう。